In Java the keyword final makes the entities unmodifiable.

Java final Keyword Example
In this section we will read about the final keyword in Java in various context.
final keyword in Java can be used with the class name, method name, and variable name. Whichever, the final keyword is used with it means that it will not later be changed. In every context in which the final keyword can be used in Java applies its main integrity i.e. unmodifiability/unchanged to all context. Including these there are additional features of final keyword that is applies when used in different-different context. Below, we are discussing on this topic in detail.
Keyword final with Class (Final classes)
In Java class can be declared as final using final keyword. If the final keyword is used in the class declaration the class becomes unable to be sub-classed. No any class can extend the final class i.e. features of a final class can't be inherited. Various classes of Java library are defined as final fro example java.lang.String, java.lang.System etc. If a final class contains the methods then these methods becomes final implicitly. In Java classes are declared as final for the security and efficiency reason. final makes the class immutable.
Syntax for declaring a class as final
public final class FinalClassName
{
......
}
But, the following class declaration type is not allowed in Java.
public class className extends FinalClass
{
......
}
Keyword final with Method
In Java method can be declared as final using final keyword. If a method is declared as final then it can't be overridden by the subclasses. Making methods to final protects it from unexpected behavior from a subclass alteration of method. If a constructor calls the method then this method should generally be declared as final because if a non-final method is called by the constructor then it may be redefined by subclass.
Syntax for declaring a method as final
public class className
{
public final void methodName1()
{
......
}
public static final void methodName2()
{
......
}
}
But, when you extends the class which contains the final method then the overriding of final method is not allowed.
public class parentClassName
{
public final void methodName1()
{
......
}
public static final void methodName2()
{
......
}
}
public class childClassName extends parentClassName
{
public void methodName1()
{
......
}
public static void methodName2()
{
......
}
}
Keyword final with Variables
In Java the final keyword can be used with the variables also. If a Java variable is declared as final and initialized by some value using an initializer or an assignment statement can not be initialized again. Initialization of variable is not required at the time of declaration. Such type of final variables are called "blank final" variable. These blank final instance variable/s must be assigned inside the constructor of the class in which they are declared. Likewise, the blank final static variable must be assigned inside the static initializer of the class in which they are declared.
Syntax for declaring a variable as final
public class AreaOfCircle {
public static final double PI = 3.141592653589793;
public final double radius = 5;
[...]
}
Syntax for declaring a variable as blank final
public class AreaOfCircle {
public static final double PI = 3.141592653589793;
public final double radius;
AreaOfCircle(double r) {
radius = r;
}
[...]
}
Example
Here an example is being given which will demonstrate you the use of final keyword in Java in various different context. In this example we will create the different classes for showing the uses of the final keyword in different context.
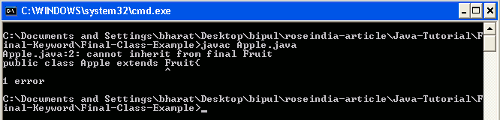
Final Class Example : In this example I have created a final class which contains some data members and their setter/getter methods then I have created another class that extends the Final class and uses the setter method to initialize the values of data members and uses the getter method to get the values of data members.
Fruit.java
public final class Fruit {
String taste;
String color;
public String getTaste() {
return taste;
}
public void setTaste(String taste) {
this.taste = taste;
}
public String getColor() {
return color;
}
public void setColor(String color) {
this.color = color;
}
}
Apple.java
public class Apple extends Fruit{
public static void main(String args[])
{
Apple apple = new Apple();
apple.setTaste("Sweet");
String taste = apple.getTaste();
apple.setColor("red");
String color = apple.getColor();
System.out.println("Apple's Color is : "+color+" and Tast is : "+taste);
}
}
Output
When you will compile the Apple.java file you will get the compilation error as follows :
Final Variable Example : In this example we will create a Java class into which we will declare a final variable and initialize that variable with some value. Then we will again try to assign a value to the final variable.
Fruit.java
public class Fruit {
public static final String taste = "Sweet";
public static final String color = "Red";
}
Apple.java
public class Apple extends Fruit{
public static void main(String args[])
{
Apple apple = new Apple();
apple.taste = "Bitter";
apple.color= "red";
System.out.println("Apple's Color is : "+color+" and Tast is : "+taste);
}
}
Output
When you compile the Apple.java file you will get the compilation error as follows :

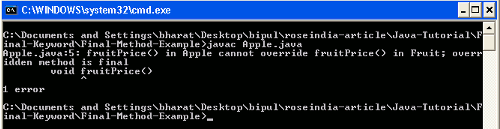
Final Method Example : In this example I have created a Java class into which I have defined a final method. Then I have created another class and extended the first class.
Fruit.java
0
public class Fruit {
String taste = "Sweet";
String color = "Red";
int price = 50;
public String getTaste() {
return taste;
}
public void setTaste(String taste) {
this.taste = taste;
}
public String getColor() {
return color;
}
public void setColor(String color) {
this.color = color;
}
final void fruitPrice()
{
System.out.println("Price of Fruit is : "+ price);
}
}
Apple.java
public class Apple extends Fruit{
int price = 100;
void fruitPrice()
{
System.out.println("Price of fruit is : "+price);
}
public static void main(String args[])
{
Apple apple = new Apple();
apple.setTaste("Sweet");
apple.setColor("red");
String color = apple.getColor();
String taste = apple.getTaste();
System.out.println("Apple's Color is : "+color+" and Taste is : "+taste);
}
}
Output
When you compile Apple.java file you will get the compilation error as follows :
1